O fraktalach

Fraktal (łac. fractus – złamany, cząstkowy, ułamkowy) w znaczeniu potocznym oznacza zwykle obiekt „nieskończenie złożony” (ukazujący coraz bardziej złożone detale w dowolnie wielkim powiększeniu). Ze względu na olbrzymią różnorodność przykładów matematycy obecnie unikają podawania ścisłej definicji. W zamian wymienia się cechy obiektów fraktalnych – najważniejsze to:

- samopodobieństwo – tzn. w skład obiektu wchodzą jego „mniejsze kopie (lub przybliżone kopie)”, np. liść paproci;
- nietrywialna struktura w każdej skali – tzn. powiększanie ujawnia kolejne równie skomplikowane formy, np. drzewo, konary, gałęzie;
- niecałkowity (a nawet niewymierny) wymiar fraktalny, np. nieskończenie długa krzywa zamknięta, która jest osadzona w ograniczonej przestrzeni (obiekt o typie „pomiędzy” linią a płaszczyzną) – przykład rzeczywisty to chociażby linia brzegowa i pomiar jej długości: im mniejsza skala pomiaru tym istotnie większy wynik.

Po raz pierwszy pojęcie fraktali zostało wprowadzone do matematyki za sprawą francuskiego matematyka i informatyka polskiego pochodzenia Benoita Mandelbrota w latach 70-tych XX wieku. Używając komputera do wizualizacji, uczynił z fraktali przedmiot intensywnych badań, przyczyniając się do lepszego ich poznania i wszechstronnego zastosowania w praktyce. Najważniejsze osoby, które istotnie przyczyniły się do rozwoju geometrii fraktalnej, to:

- Karl Weierstrass (1815 – 1897)
- Georg Cantor (1845 – 1918)
- Helge von Koch (1870 – 1924)
- Felix Hausdorff (1868 – 1942)
- Gaston Julia (1893 – 1978)
- Pierre Fatou (1878 – 1929)
- Paul Lévy (1886 – 1971)
- Benoit Mandelbrot (1924 – 2010)

Georg Ferdinand Ludwig Philipp Cantor (1845 – 1918) – niemiecki matematyk, który zainicjował (oraz znacząco rozwinął) teorię mnogości.
Zbiór Cantora jest podzbiorem jednostkowego odcinka powstającym poprzez:

- podział odcinka na 3 równe części;
- usunięcie części środkowej;
- powtórzenie procedury usuwania dla nowo powstałych odcinków.

Finalny zbiór Cantora jest zbiorem granicznym przy nieskończenie wielu iteracjach wykonanych zgodnie z powyższymi punktami.
Zbiór Cantora został opisany w roku 1883.

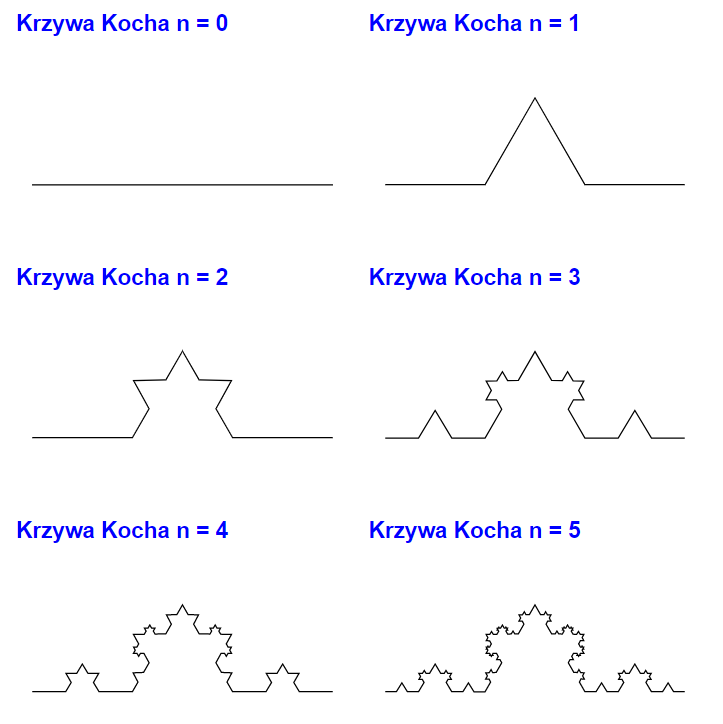
Krzywa Kocha

Krzywa Kocha jest to krzywa fraktalna. Jest ona nieskończenie długa (dla nieskończonej złożoności), ale mieści się na skończonej powierzchni. Została ona opisana po raz pierwszy w pracy "Sur une courbe continue sans tangente obtenue par une construction géométrique élémentaire" przez Helgego von Kocha w roku 1904.

Płatek Kocha

Płatek Kocha powstaje poprzez narysowanie trzech Krzywych Kocha w taki sposób, że razem tworzą jedną figurę. Tak samo jak w poprzednim przypadku możliwe jest ustawienie złożoności tak, aby rysowanie zakończyło się w określonym momencie. Oto przykładowe rysunki płatków Kocha:

Smok Heighwaya był badany po raz pierwszy przez Johna Heighwaya, Bruce’a Banksa i Williama Hartera z NASA. Fraktal ten pojawił się w powieści Michaela Crichtona Jurassic Park.

Cztery smoki, wychodzące z jednego punktu, wypełniają płaszczyznę.

Fraktale Wacława Sierpińskiego

Bardzo ciekawe i jedne z najbardziej znanych na całym świecie fraktali to dywan i trójkąt Sierpińskiego. Wacław Sierpiński to jednego z najwybitniejszych polskich matematyków żyjący w latach 1882-1969, współtwórca Polskiej Szkoły Matematycznej.

Dywan Sierpińskiego

Fraktal, który powstaje poprzez podzielenie kwadratu na 9 części i usunięcie środkowej. W kolejnym kroku ponownie dzielimy pozostałe kwadraty na 9 części i usuwamy z każdego środkową część.

Trójkąt Sierpińskiego

Konstrukcja fraktala z trójkątem jest analogiczna jak z kwadratem. Oczywiście dzielimy trójkąt na mniej części - dokładnie na 4 i usuwamy środkową. Poniżej grafika z kolejnymi krokami powstawania tego fraktala.

Odpowiednikiem trójwymiarowym Dywanu Sierpińskiego jest kostka, której konstrukcję podał austriacki matematyk Karl Menger w 1927 roku.

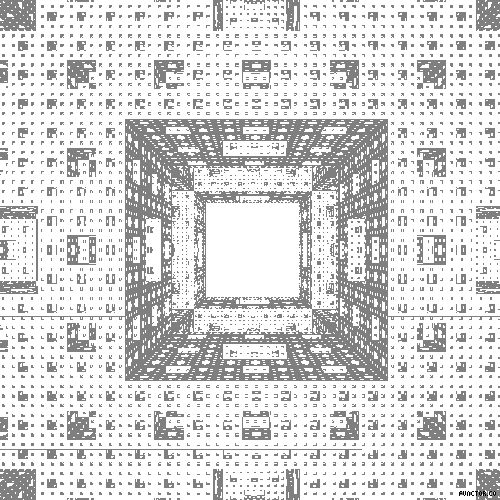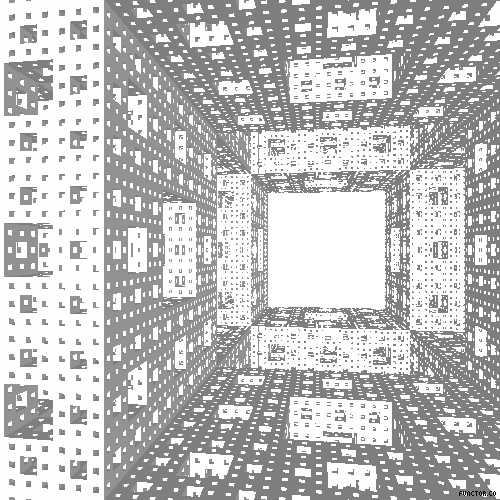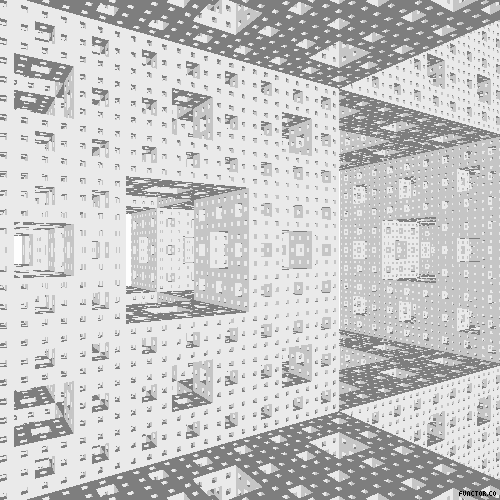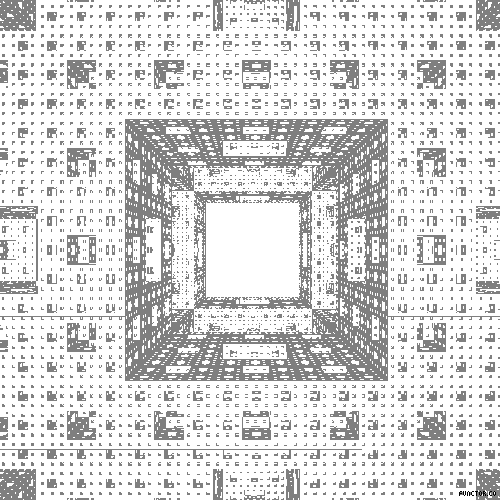
Nazwa zbioru Julii (ang. Julia Set) pochodzi od nazwiska jego odkrywcy - francuskiego matematyka Gastona Julii. Brzeg tego zbioru jest fraktalem.

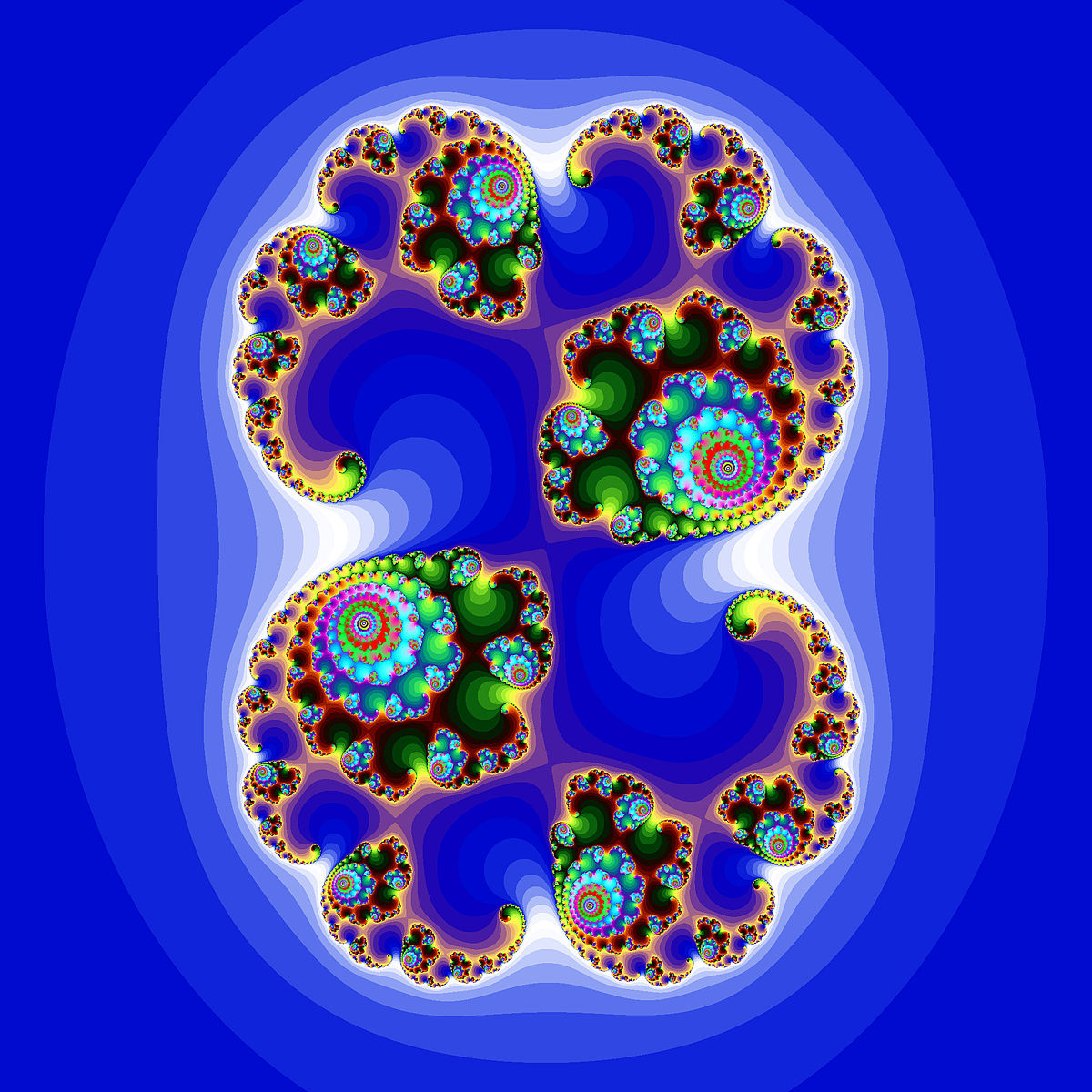
Zbiór Mandelbrota (żuk Mandelbrota) – podzbiór płaszczyzny zespolonej, którego brzeg jest jednym z najbardziej znanych fraktali, „najsłynniejszym obiektem współczesnej matematyki”. Nazwa tego obiektu została wprowadzona dla uhonorowania jego odkrywcy, francuskiego matematyka Benoit Mandelbrota.

Autor: Marta Hering-Zagrocka